1
2
3
4
5
6
//二维数组A[b1][b2]中元素Aij的起始地址为：
LOC[i,j]=LOC[0,0]+(b2*i+j)  L
//三维数组A[b1][b2][b3]中数据元素A[i][j][k]的起始地
址为：
LOC[i,j,k]=LOC[0,0,0]+(b2*b3*i+b3*j+k)*L

矩阵的压缩存储

特殊矩阵

上下三角矩阵：利用矩阵的特殊结构进行降维存储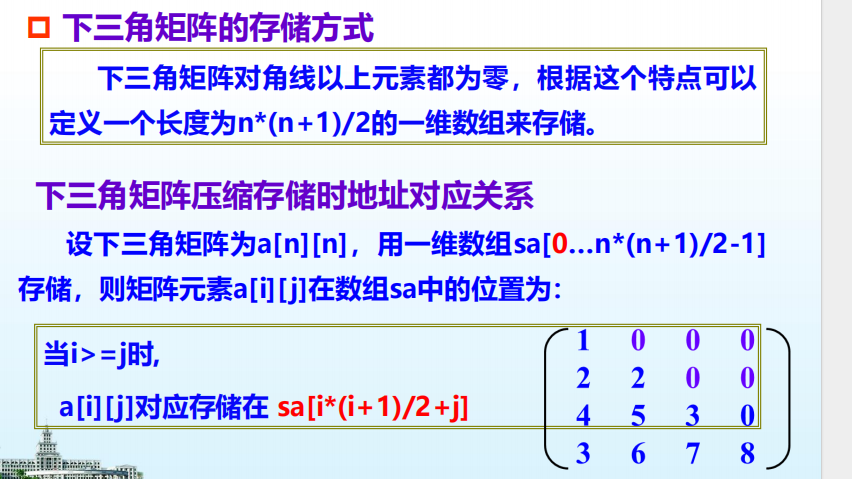image-20241125200614453

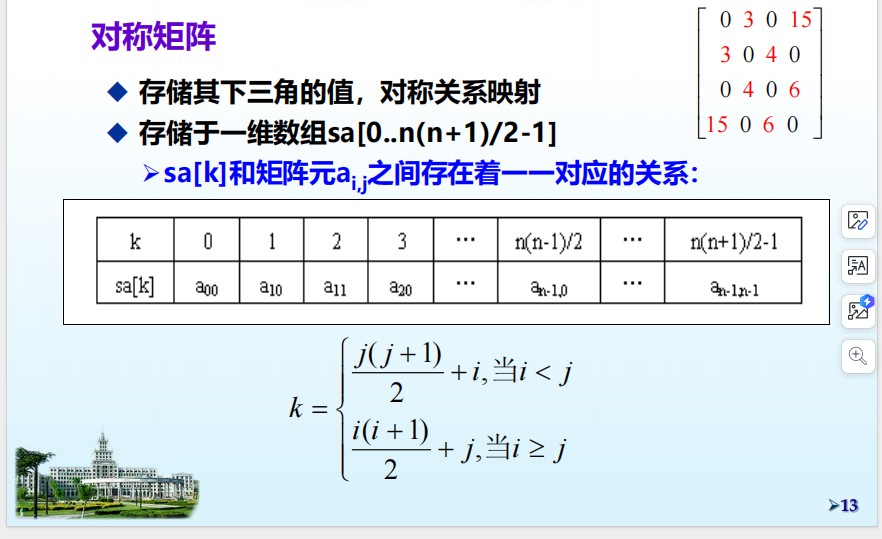
对称矩阵：存在降维的下三角矩阵里，然后对称映射

image-20241125201459375

稀疏矩阵

image-20241125202133776

三元组表示：只存储非零元素的 行 列 值

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define MAXSIZE 12500
typedef struct
{
    int i,j; //row and column
    ElementType e; //value
}Triple_node;

typedef struct
{
    Tripe_node [MAXSIZE+1];
    int mu ,nu ,tu;
}TSMatrix;

TSMartix M;

矩阵的压缩存储

三元组的转置

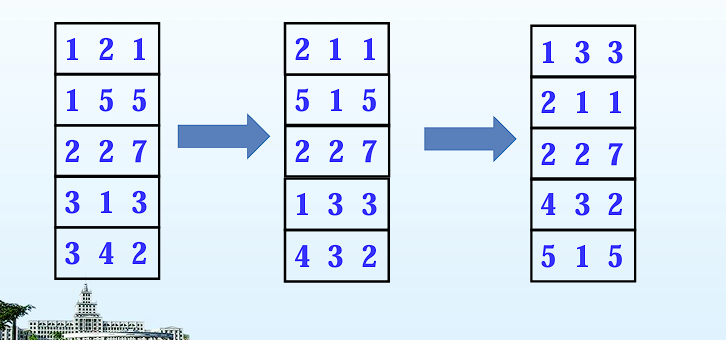
普通方法：最后一列代表元素的值，不变——>前两列转过来——>进行排序，以行为基准

一步实现：直接对第二列进行扫描，从小到大进行转置并放到新的三元组

​ 高复杂度：每次都对第二列进行扫描，选出当前数值最小的（时间复杂度 nu*tu）

​ 低复杂度：只扫描一遍第二列，记录转置之后每一行有几个元素，然后计算出转置之后每行开始存的的首地址

image-20240918102538589

广义表

表头：第一个元素

表尾：除了表头以外其他元素组成的表

image-20241126173845577

因此，gethead 取出的是元素（使用后最外一层括号已经去掉），gettail 取出的是广义表（使用后括号层数不变）

v

广义表的特点

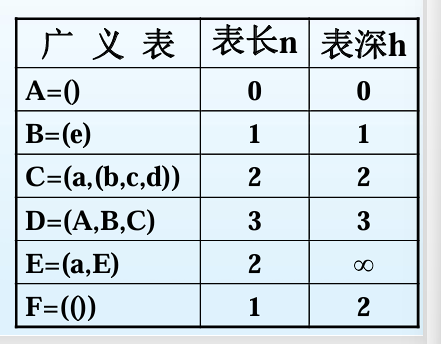
① 广义表中的元素可以是原子也可以是子表，广义表是一个多层次结构

② 广义表是可以共享的。如广义表B是D的子表

③ 广义表允许递归，如广义表E是一个递归表

④ 广义表的元素间存在次序关系和层次关系，广义表展开后包含的 括号层数称为广义表的深度。如C的深度为2，E的深度为 infinity

广义表的存储结构

  1. 头尾指针结点结构

image-20241126174218547

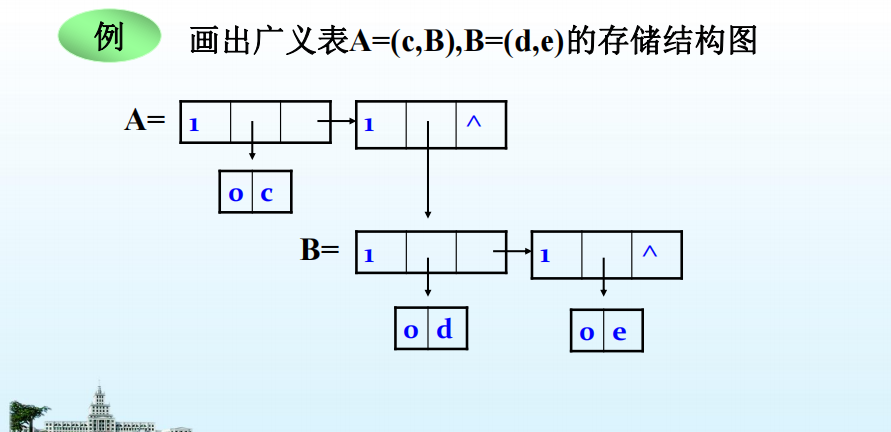
image-20241126191603999

2.

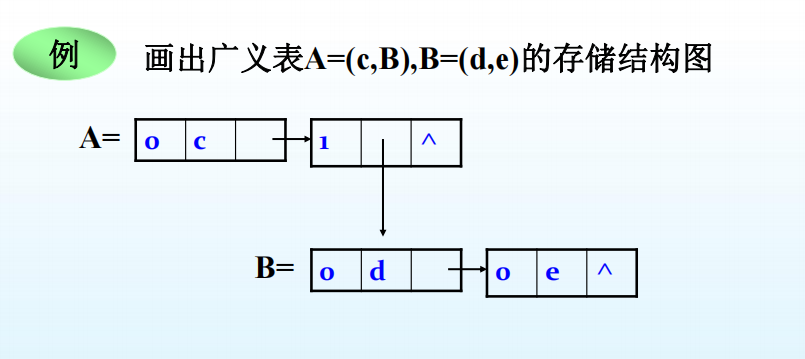
扩展头尾指针结点结构

image-20241126191817080

image-20241126191826122