二叉树的性质

  • n = n0 + n1 +n2

  • n0 = n2 +1

  • n-1 = n1 + 2*n2（总度数为n-1）

  • 满二叉树： 满的

  • 完全二叉树：现有的节点编号和满二叉树的一致

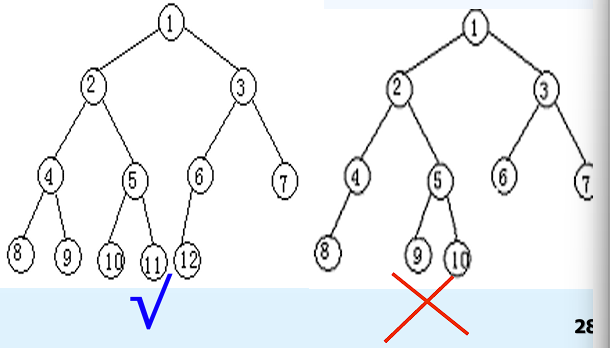
    image-20240923141022960

  • 具有n个结点的完全二叉树的深度为image-20240923141344836

  • 已知编号i,求双亲的编号？（完全二叉树）

​ i/2 向下取整

  • 已知编号i，左孩子的节点是2i，右孩子是2i+1

    二叉树的存储结构

    顺序存储结构

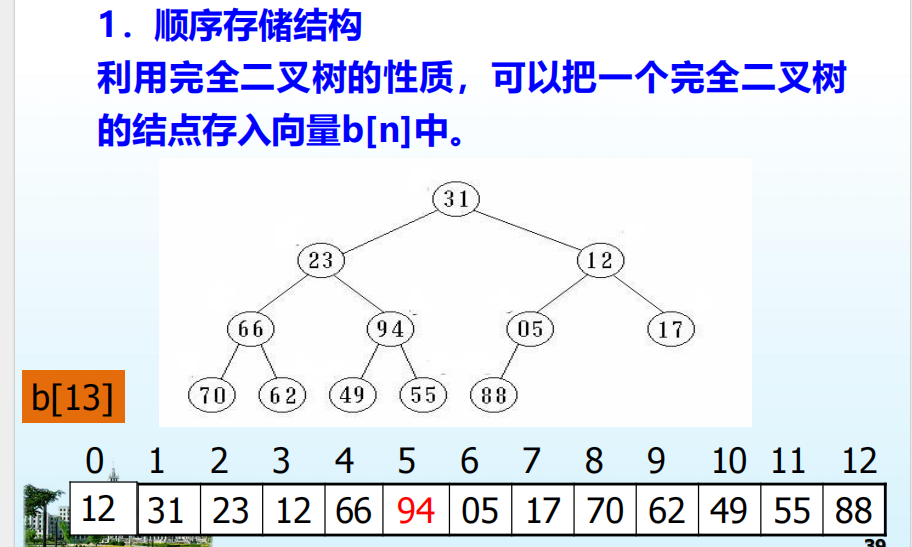
    image-20241126200632995

    链式存储结构

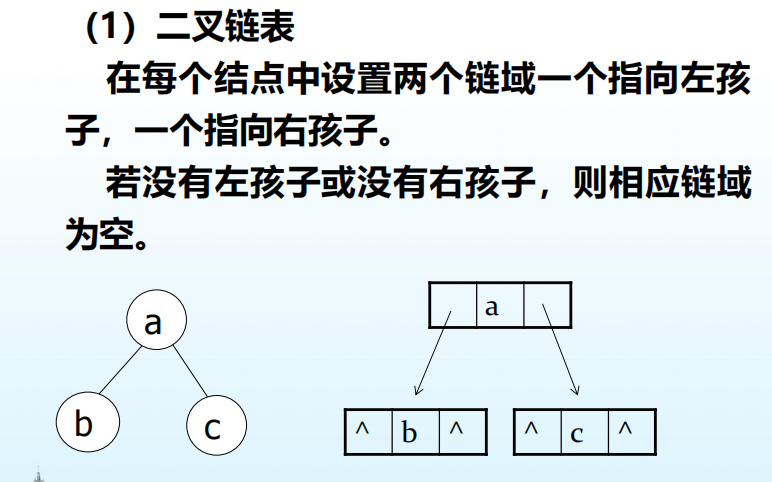
    image-20241126200733448

    n个结点的二叉树链式存储中，共有n+1个空指针域

    证明：n个结点的二叉树，除了根节点以外，其余的结点都有上一个双亲结点指来的指针，因此一共有n-1个指针域被利用，所以剩下了n+1个指针域为空

    二叉链表缺点：很难找到双亲结点
    带双亲指针的二叉链表（三叉链表）

    image-20241126202059907

    遍历二叉树

    遍历的递归算法

    image-20241126203450680

    image-20241126203459533

    image-20241126203509644

    遍历的非递归算法

    先序遍历

    先序遍历：相当于第一次遇到元素就直接遍历

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    void PreOrder(BiTNode *root)
    {
        BiTNode *p,*node[MAX]; //p用来更新当前指向的结点  node[]用来当栈
    	int top = 0;
        p = root;
        do{
            while(p!=NULL) //一直滑到最左边
            {
                visit(p->data);//直接开始遍历
                node[top] = p; //入栈
                top ++;
                p = p->lch;
            }
            if(top>0) //既然滑到了最左边，那说明之前滑过去的已经遍历完了，直接回退最后一次的null，然后指向最左边节点的右孩子
            {
                top --;
                p = node[top];
                p = p->rch;
            }        
        }while(!(top == 0 && p==NULL)) //只有当栈为空，且p指向null的时候，才标志着遍历结束

    }
    中序遍历

    中序遍历：相当于第二次遇到元素的时候执行操作

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    void MidOrder(BiTNode *root)
    {
    	BiTNode *p,*node[MAX]; //p用来更新当前指向的结点  node[]用来当栈 
    	int top = 0;
        p = root;
        {
            while(p!=NULL)
            {
                node[top] = p;
                top++;
                p = p->lch;
            }
            if(top>0)
            {	
                top--;
                p = node[top];
                visit(p->data);
                p = node[top]->rch;
            }        
        }while(!(top==0 && p==NULL));
    }
    后序遍历

    后序遍历：相当于第三次碰到元素的时候进行操作

例题

1.计算节点个数

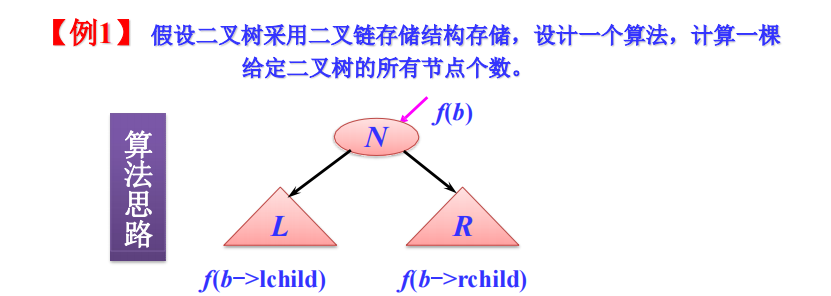
image-20241127003226931

  • 二叉树nb的地方，就在于它的结构，容易实现递归
  • 因此，可直接设置递归：
  • 如果f(b) == NULL,那f(b) = 0;(递归终止条件)
  • 如果f(b)!=NULL,那f(b) = f(b->lch)+f(b->rch)
1
2
3
4
5
6
7
8
9
10
11
12
13
int compute_node(BitTree *node)
{

	if(node->data == NULL)
	{
		return 0;
	}
	else
	{
		int count = compute_node(node->lch)+compute_node(node->rch);
		return count +1;//别忘了把自己加上
	}
}

2.计算叶子节点个数

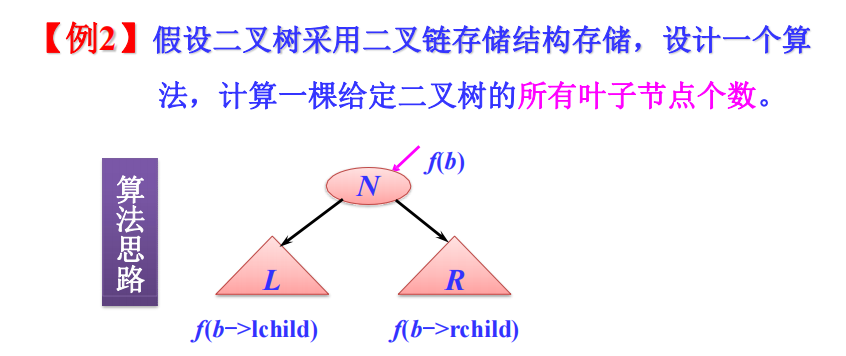
image-20241127003904677

  • 同上一题一样，只不过是改改返回时的条件
  • 只有当一个节点没有左节点和右节点的时候，再把它算数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int compute_yezi(BiTree *node)
{
    if(node == NULL) //放在最前面判断，防止空指针产生错误
    {
        return 0;
    }
    else if(node->lch || node->rch)
    {
        return (compute_yezi(node->lch) + compute_yezi(node->rch));
    }
    else 
    {
        return 1;
    }
}

3.复制二叉树

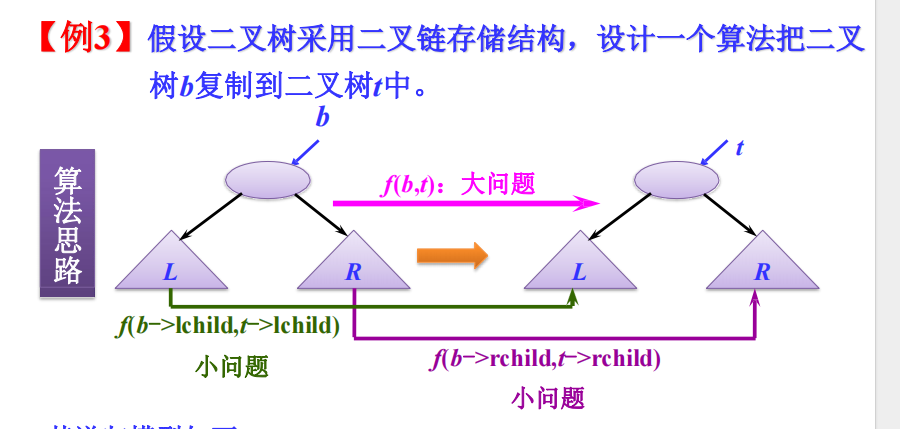
image-20241127004644915

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void copy_tree(BiTree *backup,BiTree *copy)
{
    if(backup == NULL)
    {
        copy == NULL;
    }
    else
    {
        copy = (BTNode*)malloc(sizeof(BTNode)); //分配内存空间
        copy->data = back_up->data;
        copy_tree(backup->lch,copy->lch);
        copy_tree(backup->rch,copy->rch);
    }
}

4.交换左右子树

image-20241127082721170

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void change(BiTree *backup,BiTree *change)
{
    if(node == NULL)
    {
        
    }
    else
    {
        change = (BTNode*)malloc(sizeof(BTNode));
        change->data = back_up->data;
        //======下面的与复制不同，是反的====
        change(backup->lch,change->rch);
        change(backup->rch,change->lch);
		//==============================
    }
}

5.构建二叉树

image-20241127084354935

  • 非递归求解的话，就要用到栈
  • 递归求解比较简洁
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void creat_tree(BiTree *node,char*s)
{	
    int i = 0;
	while(i<strlen(s))
    {
        if(s[i] == '#')
        {
            node = NULL;
        }
        else
        {
            node = (BiTNode*)malloc(sizeof(BiTNode));
            node->data = s[i];
            creat_tree(node->lch);
            creat_tree(node->rch);
        }
    }
}

6.求二叉树高度

image-20241127090727823

  • 别什么都想扯到遍历上，要有递归的“分治思想”

  • 二叉树的高度，就是左子树和右子树中，更高的那一支的高度加一，可以用递归求解

1
2
3
4
5
6
7
8
9
10
11
12
13
int height(BiTree t) //因为不需要做修改，所以直接传参即可
{
    if(t == NULL)
    {
        return 0;
    }
    else
    {
    	int h1 = height(t.lch);
    	int h2 = height(t.rch); 
        return max(h1,h2);
    }   
}

7.删除二叉树

image-20241127091633041

1
2
3
4
5
6
7
8
9
void destory(BitTree *t)
{
	if(t != NULL)
	{
		destory(t->lch);
		destory(t->rch);
		free(t);
	}
}
  • 只能使用类后序遍历的方法，因为节点信息必须最后删除，不然信息会丢失